While I've read countless articles about health-related issues like eating right, getting enough sleep, exercise, etc., I still read recently published articles on these topics. Why?
Because the article may contain new information, it may simply reinforce what I think I already know, or it may remind me of something that I had forgotten.
With that said, this article is going to discuss potato seed-piece size-a topic I'm sure you've read about numerous times. This time, however, I'd like to look at how seed-piece size may impact your operating costs. And, who doesn't want to keep those to a minimum?
What something costs depends on a number of factors. Seed is no different because the cost depends on the variety, transportation, seed treatment and cutting costs, etc.
For many varieties, seed-pieces should be in the range of 1.5 to 2.5 oz. with an average seed-piece size of 2 oz. Granted, increasing seed-piece size may result in more yield, but then the law of diminishing returns kicks in, meaning that for every incremental increase in seed-piece size, there is less increase in yield resulting from the additional size.
Furthermore, planters may not be able to accurately plant seed-pieces that are larger than approximately 3 oz.
To discuss economics, let's assume seed costs $11 per cwt by the time you get it to the field ready to plant, and you are planting seed-pieces 12 inches apart in 36-inch rows. If the planter achieved 100 percent accuracy, there would be 14,520 seed-pieces per acre. But, all potato planters will have some skips, so we'll assume 90 percent displacement, or 13,068 seed-pieces.
Now, let's go through the calculations to determine seed cost per acre using an average seed-piece size of 2 oz.
2.0 oz/seed-piece x 14,520 seed-pieces/ac ÷ 1600 [(to convert oz/ac to cwt/ac) or 18,15 cwt/ac] x .90 accuracy x $11.00/cwt = $179.69/ac.
If the average seed-piece size is 2.5 oz, the cost increases to $224.61 per acre. Up the average seed-piece size to 3 oz and the cost swells to $269.53, a 50 percent increase.
With the assumptions above, each one-half ounce increase in average seed-piece size adds an additional $45 per acre. For 500 acres of potatoes, each one-half ounce increase in average seed-piece size adds $22,500 to your seed bill. Increasing average seed-piece size by just one-quarter ounce would increase costs $11,250 on 500 acres.
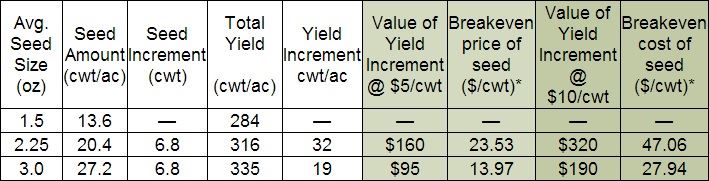
To further illustrate the economics of seed-piece size, compare the yield data of Russet Norkotah potatoes from small-plot research at University of Idaho Aberdeen Research and Extension Center in the accompanying table.
At any given price for the harvested crop, the break-even price you can pay for seed decreases as the average seed-piece size increases.
For example, at a $5/cwt return, you could afford to pay $23.53/cwt for seed with an average seed-piece size of 2.25 oz. compared to 1.5, but only $18.75/cwt if you wanted to increase the average seed-piece size from 1.5 to 3 oz. with all other production factors remaining unchanged.
The above discussion is for illustrative purposes only. The questions you need to ask yourself are: Will the additional production on my farm, if any, pay for the added expense of planting larger seed pieces, and will the planter accurately plant the seed size selected?
In today's economy, it's important to keep your costs to a minimum. Depending on location and other production factors, seed costs account for about 16 percent of the total operating budget to raise potatoes. It just makes sense to keep seed costs as low as possible without affecting yield and quality.
* Note: this is the price per cwt you could pay for the extra 6.8 cwt of seed per acre based on the incremental increase in yield and the specified value of the potatoes. The price you could pay for seed going from 1.5 to 3.0 oz would be the average of the two breakeven values shown.